有序多分类剂量反应资料Meta分析中原始研究参照组转换及软件实现

引用本文

周权, 郭鹏, 钟国超, 钟山亮. 有序多分类剂量反应资料Meta分析中原始研究参照组转换及软件实现.循证医学, 2015,16(1): 60-64
ZHOU Quan, GUO Peng, ZHONG Guo-chao, ZHONG Shan-liang. Transforming the Reference Group of Discrete Correlated Data in Original Study of Dose-Response Meta-Analysis. Journal of Evidence-based Medicine, 2015,16(1): 60-64 复制到剪切板

Permissions

有序多分类剂量反应资料Meta分析中原始研究参照组转换及软件实现

周权¹, 郭鹏², 钟国超³, 钟山亮⁴

1. 常德市第一人民医院科教科,湖南常德 415003

2. 遵义医学院第三附属医院普外科, 贵州遵义 563000

3. 重庆医科大学附属第二医院肝胆外科, 重庆 400010

4. 江苏省肿瘤医院临床检验中心, 南京 210009

通讯作者：钟山亮, Tel: 025-83283334; E-mail: seuzsl@163.com 作者简介：

作者简介：周权(1987-),男,湖南常德人,医学硕士,研究方向为流行病与卫生统计学。

基金:常德市科技局指导基金资助项目(2014ZD11)

摘要

目的介绍剂量反应Meta分析原始研究有序多分类资料参照组转换的方法。方法以队列研究为例介绍参照组转换的原理,并结合实例数据,利用EXCEL与R两种软件分别独立实现参照组转换。结果两种软件实现转换的结果一致,与原始数据再次分析结果相似。结论在无法获取原始研究数据的情况下,利用EXCEL与R两种软件都能很好地解决有序多分类资料参照组转换的问题。

关键词: 剂量反应Meta分析; 转换; EXCEL软件; R软件

中图分类号:R195.1 文献标识码:A 收稿日期:2015-06-25

Transforming the Reference Group of Discrete Correlated Data in Original Study of Dose-Response Meta-Analysis

ZHOU Quan¹, GUO Peng², ZHONG Guo-chao³, ZHONG Shan-liang⁴

1. Department of Science and Education, The First People’s Hospital of Changde, Hu’nan Changde 415003, China

2. General Surgery, The Third Affiliated Hospital of Zunyi Medical University, Zunyi Medical University, Guizhou Zunyi 563000, China

3. Department of Hepatobiliary Sugery, Chongqing Medical University,Chongqing 400010, China

4. Center of Clinical Laboratory Science, Jiangsu Cancer Hospital, Nanjing 210009, China

Abstract

ObjectiveTo introduce the method and software of transforming the reference group of discrete correlated data in original study of dose-response meta-analysis.Method It was illustrated on a cohort study data. Firstly, introduce the transforming theory. Then we conducted the transforming using EXCEL and R softwares.Result The result was consistent between two softwares and reanalyzing the original data.Conclusion EXCEL and R softwares can be a good solution to transforming the reference group of discrete correlated data in original study of dose-response meta-analysis, in case of failing obtaining the original data.

Key words: dose response meta-analysis; transform; EXCEL software; R software

Show Figures

剂量反应关系Meta分析是一类新型的Meta分析方法, 相比常见的二分类及连续性资料Meta分析, 此类研究可估计暴露因素与疾病的剂量反应关系^[1]。随着方法学的日益成熟, 国内外运用此方法进行分析的文章越来越多^{[2, 3, 4, 5, 6]}。之前笔者所在研究团队已介绍过利用三种软件实现此类Meta分析的方法^{[1, 7, 8]}, 但在实际分析过程中, 经常会遇到这样的情况:多数原始研究均以最低剂量组为参照组, 而少数原始研究却以其它组别为参照, 这两类研究是不能直接合并的, 要合并就必须将少数以其它组别作为参照的原始研究转换为以最低剂量组作为参照的情况。本文就如何实现这一转换作一介绍, 以期为解决此类问题提供方法学指导。

1 思路与原理

1.1 处理思路

流行病学研究中探讨多暴露水平与发生某类结局(疾病)关系的情况, 研究结果常呈现以下信息:①多因素统计分析调整多种混杂后, 以最低或最高水平暴露组为参照, 其他组别均与之对比的效应量[比值比(odds ratio, OR)或相对危险度(relative risk, RR)]及95%可信区间(confidence interval, CI); ②同时提供各级暴露水平发生与不发生某类结局的例数。为了使各研究参照方向处理一致, Greenland 和 Longnecker^[9]提出了一种解决方案:先利用原始研究中提供的数据①与数据②通过数学规划求解产生一组模拟校正混杂后的各级暴露水平发生与不发生某类结局的伪有效例数, 再利用这些伪有效例数估计任一参考情况下的各级暴露发生某类结局的效应量(OR或RR)及其95%CI。

1.2 基本原理

此转换主要应用于流行病学研究中的病例对照研究､队列研究二种类型, 本文以队列研究为例对其基本原理作一介绍, 病例对照研究情况可依此类推。

队列研究常以表1的形式呈现研究数据, B₀表示非暴露组人数或人年, Bi表示不同水平暴露组人数或人年, A₀表示非暴露组发生研究结局的人数或人年, A_i表示不同水平暴露组发生研究结局的人数或人年。

表1 队列研究中研究数据报告格式

通过公式(1)可以计算不同水平暴露组相对于参照组的效应量RR的自然对数

$\log_{e} (R_{i}) = \log_{e} (\frac{A_{i} B_{0}}{A_{0} B_{i}})$ (1)

通过公式(2)可以计算不同水平暴露组相对于参照组的效应量RR自然对数方差

$V_{i} = \frac{1}{A_{0}} - \frac{1}{B_{0}} + \frac{1}{A_{i}} - \frac{1}{B_{i}}$ (2)

通过公式(3)可以计算不同水平暴露组相对于参照组的效应量RR自然对数的95%CI

$\log_{e} (R_{i}) \pm 1.96 \sqrt[]{V_{i}}$ (3)

另外还需要利用表1数据计算一下P值:非暴露组人数或人年与所有研究暴露人数或总人年的比值和Z值:所有研究暴露人数或总人年与所有发生结局人数的比值。因为一般原始研究结果都会提供不同暴露水平校正的RR值, 结合A0､B0已知的情况下, 利用公式(1)就可以变换成公式(4)

B_i= $\frac{A_{i} B_{0}}{A_{0} B_{i}}$ (4)

在公式(4)中Ai仍然是未知项, 前面介绍一般原始研究结果还会提供不同暴露水平校正RR值的95%CI, 那么利用公式(3)就可以推算出效应量RR自然对数方差, 再将公式(4)代入公式(2)中即可求出Ai, 公式(5)

A_i= $(R_{i} \frac{A_{0}}{B_{0}} - 1) \div (V_{i} + \frac{1}{A_{0}} - \frac{1}{B_{0}})$ (5)

将公式(5)代入公式(2)即可求出Bi, 公式(6)

B_i= $(\frac{B_{0}}{A_{0} R_{i}} - 1) \div (V_{i} + \frac{1}{A_{0}} - \frac{1}{B_{0}})$ (6)

在此基础上, 再计算P[′ ]与Z[′ ]

利用从表1中获得的P值和Z值, 对下面公式(9)进行迭代, 使公式(9)无限接近于0便可得到估算的A0与B0值,

${(\frac{p - p^{'}}{p})}^{2} + {(\frac{z - z^{'}}{z})}^{2}$ (9)

通过上述公式便可求得一组模拟校正混杂后的各级暴露水平发生与不发生某类结局的伪有效例数, 这组数据不具有实际的意义, 但通过它们计算出的RR值却与原始研究多因素分析得出的结果基本类似(以上公式均来自于Hamling等研究论文及其附录材料^[10])。

2 实例分析

2.1 数据来源

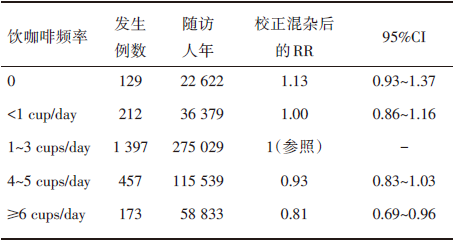
本文研究数据来自于Discacciati等^[11]2013年发表的一项关于饮用咖啡与前列腺癌风险的队列研究, 该研究通过对44 613名45~79岁的瑞典人进行了为期13年的随访, 其中有2 368人发生了早期局限性前列腺癌。原文报道饮用咖啡数量与发生早期局限性前列腺癌的结局如表2所示。因为原文并非利用常规的最低剂量组(0)或最高剂量组(≥ 6 cups/day)进行分析, 而是采用了一个中间组(1~3 cups/day)作为参照。纳入这样的数据进行剂量反应Meta分析, 在向作者寻求数据无果的情况下, 就只能利用现有数据对参照组进行转换, 将其转换以最低组或最高组为参照后再和其他研究进行剂量反应Meta分析。

表2 饮用咖啡与早期局限性前列腺癌发生实例数据

2.2 运行EXCEL宏文件对参照组进行转换

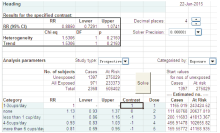
根据Greenland 和 Longnecker^[9]提出的理论, Hamling等^[10]将其制作成了一个EXCEL宏文件可很方便地实现上述转换。EXCEL程序和帮助文件可从“ http://www.pnlee.co.uk/software.htm” 网站上免费下载。从网站上下载此EXCEL宏文件后, 用office2010以上版本打开, 录入表2中的校正混杂后RR及CI数值､非暴露组(1~3 cups/day)早期局限性前列腺癌病例数和随访人年以及所有暴露组(0､< 1 cup/day､4~5 cups/day､≥ 6 cups/day)病例数总数和随访总人年, 表格中Contrast赋值范围是0､-1､1, 其功能是进行参照组和比较组的设定:取值为0代表参照组､取值为1代表比较组, 取值为-1代表忽略此组分析。这里先设定“ 不喝咖啡组” 为参照, 赋值为“ 0” , “ 1~3 cups/day组” 为比较组, 赋值为“ 1” , 其他组别暂不参与分析, 赋值为“ -1” , 设定研究类型为“ Prospective” 分类水平是“ Exposure” , 点击“ Solve” 按钮, EXCEL将进行规划求解, 自动找到最佳的解。在EXCEL表格左上角“ Results for the specified contrast” 部分显示出“ 1~3 cups/day组” 与“ 不喝咖啡组” 相比较的RR值及95%CI。依次将< 1 cup/day､4~5 cups/day､≥ 6 cups/day组的Contrast值设定为1, 再分别进行三次运算, 便可以将原来以1~3 cups/day组为参照的RR值及95%CI转换为以“ 不喝咖啡组” 为参照的情况了(图1)。同样如果想转换为以其他组别为参照的情况, 可以依照上面的操作步骤进行。

	Figure Option View Download New Window
	图1 EXCEL 宏文件进行参照组转换过程

2.3 运行R软件对参照组进行转换

R软件安装好后, 先在电脑中的任意盘(如D盘)建一个名为Rworkplace文件夹, 同时在桌面的R软件图标上单击右键选择“ 属性” , 将“ 起始位置” 修改为:D:\Rworkplace, 以后R软件运行的所有数据都会自动储存在这个文件夹中^[12]。运行R软件, 点击 “ Packages” 下拉菜单后, 再选“ Set CRAN mirror” , 会出现下载数据源的镜像列表, 然后选择离自己距离最近的镜像, 如China(Beijing1)然后在连网的状态下, 在命令窗口输入相应代码可自动安装和加载dosresmeta软件包。

install.packages(c(“ mvmeta” , “ dosresmeta” ))

library(“ dosresmeta” )

将表1纵标目转换为英文名称后录入EXCEL中, 另存为CSV(逗号分隔)文件, 存入之前建立的D:\Rworkplace 文件夹中。利用read 函数读入之前建立好的EXCEL数据集, 相应的命令是:

pca< -read.csv(“ pca.csv” )

先对表1中RR取自然对数, 并求相应的标准误, 再利用dosresmeta程序包中的hamling函数获得校正混杂后各级暴露水平发生与不发生某类结局的伪有效例数, 相应的命令如下:

pca$logrr=log(pca$rr)

pca$lnLL=log(pca$ll)

pca$lnUL=log(pca$ul)

pca$se=(pca$lnUL-pca$lnLL)/3.92

hamling(logrr = logrr, se = se, cases = cases, n = peryears, type = type, id = id, data = pca, order = T)

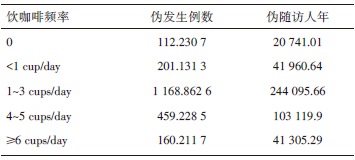
运行后结果如表3所示。

表3 饮用咖啡与早期局限性前列腺癌发生的伪有效例数

再利用epitools程序包中的epitab函数计算以不喝咖啡为参照情况下各级暴露发生早期局限性前列腺癌的效应量RR及95%CI。

## 安装和加载epitools程序包

install.packages(c(“ epitools” ))

library(epitools)

## 录入表3中的数据

zq< -matrix(c(112.2307, 20741.01, 201.1313, 41960.64, 1168.8626, 244095.66, 459.2285, 103119.9, 160.2117, 41305.29), 2, 5)

## 添加横纵标目

dimnames(zq) < -list(Outcome = c(“ cases” , “ peryears” ),

“ Antibody level” = c(“ none” , “ < 1cups” , “ 1-3cups” , “ 4-5cups” , “ > =6cups” ))

##对行列数据进行转置

zq < - t(zq)

##利用epitab函数进行分析, method=“ ” 可取值为“ oddsratio” ､“ riskratio” ､“ rateratio” 分别代表对病例对照研究求解RR值, 累积队列研究求解RR值, 人年队列研究求解RR值。verbose=TRUE代表显示详细的计算过程。

epitab(zq, method=“ rateratio” , verbose = TRUE)

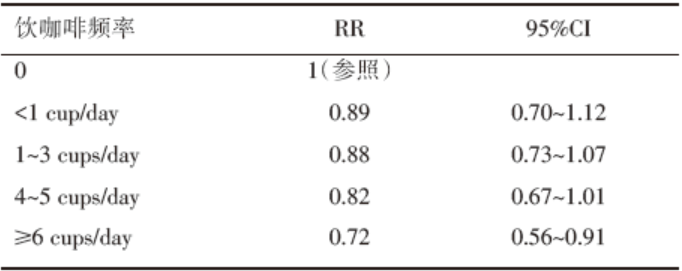
运行后结果如表4所示, 与EXCEL软件运算所得的各咖啡饮用频率组早期局限性前列腺癌发生的效应量及95%CI一致, 与原文献作者重新以不喝咖啡为参照分析的结果也基本一致^[13]。

表4 以不喝咖啡组为参照时饮用咖啡与早期局限性前列腺癌发生的效应量

3 讨论

队列研究或病例对照研究中常常会遇到有序多分类暴露与结局RR或OR数据资料, 常规的Meta分析方法只能提取两个组别数据(一般取最高剂量相对最低剂量的RR值或OR值进行合并), 这种做法极大地浪费了中间组别数据的检验效能。而剂量反应Meta分析可直接纳入所有组别进行分析, 并可估算暴露因素与疾病发生的剂量反应关系。在实施的过程中, 又可能遇到了新的问题:当多数原始研究均以低剂量为参照组, 而少数原始研究却以其它组别为参照, 最好的解决方案是联系原始研究的作者, 让其以最低剂量为参照再次分析后将结果返回。这种方法估计十有八九会毫无所获, 特别是那些年代久远的文献, 要联系到原作者重新分析数据几乎不可能。在这种情况下一种专门针对数据转换的方法便应运而生了:由Greenland 和 Longnecker教授^[9]最先阐述了转换的原理, Hamling教授编制了专门的EXCEL宏文件和SAS宏命令来实现转换, 近年来, 随着R软件的广泛运用, 瑞典生物统计学家Alessio Crippa开发专门的剂量反应Meta程序包“ dosresmeta” 其中的hamling()函数也能很方便的实现该转换, 但目前剂量反应Meta运用最广泛的分析软件STATA却没有此程序进行转换。故本文详细阐述了这一转换的原理, 并结合实例数据进行分析。

本文利用了两种软件进行分析, 两种软件都可以单独实现转换, 转换的结果是一致的。Discacciati教授曾对原始数据重新分析结果与EXCEL转换后的数据做比较, 发现二者数据基本一致[13], 此转换可基本模拟转换参照组后原始研究的多因素分析结果。将EXCEL转换后得到的伪有效例数与效应量及95%CI替换原始文献中提供的数据, 与其他原始研究结果一起放入STATA软件就可以进行剂量反应Meta的分析。R软件剂量反应Meta程序包“ dosresmeta” 转换更是将此转换内置为一个可选择的参数, 只需在分析时将协方差矩阵估算方法covariance=“ ” 选择为“ h” (hamling)便可一步到位的处理剂量反应数据。

进行参照组转换时, 根据原始数据计算伪有效例数从数学运算上来看就是一个规划求解的过程, 也就是寻求使本文公式(9)接近于零时的最优解。进行分析时, 有时会出现找不到最优解的情况, 主要是以下两个原因:①求解方程从初始值开始运算使公式(9)接近于零, 但达不到应有的精确度, ②从初始值进行运算, 始终找不到最优解。第一种情况比第二种情况更为常见, 这时只需要调整一下精确度就可以了, 如:把EXCEL表格中Solver Precision下拉框数值如从0.000 01调整到0.001, 再重新求解就可以了。如调整精确度还不能解决的话就可能是第二种情况了, 这里要先认真核对原始文献中的数据是否抄录有误, 必要时运用一些检查公式^[14]对原始文献中报道数据的真实情况进行检查, 或是将初始数据(四格表中的非暴露组病例数和随访人年数), 做一下细微的调整。

本文只介绍了队列研究的参照组转换公式与软件实现过程, 实际与病例对照研究数据的转换过程类似, 具体公式和操作方法可参考EXCEL宏文件的帮助说明书和R软件“ dosresmeta” 程序包说明书, 总之运用EXCEL和R两种软件均可实现对原始数据参照组的转换, 转换结果一致, 可自行选择使用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	周权, 李卉, 罗美玲, 等. 剂量反应关系Meta分析在R软件中的实现[J]. 现代预防医学, 2015, 42(5): 789-794. [本文引用:2]
[2]	Orsini N, Li R, Wolk A, et al. Meta-analysis for linear and nonlinear dose-response relations: Examples, an evaluation of approximations, and software[J]. Am J Epidemiol, 2012, 175(1): 66-73. [本文引用:1]
[3]	Crippa A, Discacciati A, Larsson SC, et al. Coffee consumption and mortality from all causes, cardiovascular disease, and cancer: A dose-response meta-analysis[J]. Am J Epidemiol, 2014, 180(8): 763-775. [本文引用:1]
[4]	Liao WC, Tu YK, Wu MS, et al. Blood glucose concentration and risk of pancreatic cancer: Systematic review and dose-response meta-analysis[J]. BMJ, 2015, 349: g7371. [本文引用:1]
[5]	Wang X, Ouyang Y, Liu J, et al. Fruit and vegetable consumption and mortality from all causes, cardiovascular disease, and cancer: Systematic review and dose-response meta-analysis of prospective cohort studies[J]. BMJ, 2014, 349: g4490. [本文引用:1]
[6]	Zhong S, Chen W, Yu X, et al. Coffee consumption and risk of prostate cancer: An up-to-date meta-analysis[J]. Eur J Clin Nutr, 2014, 68(3): 330-337. [本文引用:1]
[7]	罗美玲, 林希建, 刘如春, 等. 剂量反应关系Meta分析在Stata软件中的实现[J]. 循证医学, 2014, 14(3): 182-187. [本文引用:1]
[8]	周权, 罗美玲, 王冕, 等. 应用SAS软件宏命令实现剂量反应关系Meta分析[J]. 循证医学, 2015, 15(1): 54-59. [本文引用:1]
[9]	Greenland S, Longnecker MP. Methods for trend estimation from summarized dose-response data, with applications to meta-analysis[J]. Am J Epidemiol, 1992, 135(11): 1301-1309. [本文引用:3]
[10]	Hamling J, Lee P, Weitkunat R, et al. Facilitating meta-analyses by deriving relative effect and precision estimates for alternative comparisons from a set of estimates presented by exposure level or disease category[J]. Stat Med, 2008, 27(7): 954-970. [本文引用:2]
[11]	Discacciati A, Orsini N, Andersson SO, et al. Coffee consumption and risk of localized, advanced and fatal prostate cancer: A population-based prospective study[J]. Ann Oncol, 2013, 24(7): 1912-1918. [本文引用:1]
[12]	罗美玲, 谭红专, 周权, 等. 在R软件中实现单个率的Meta分析[J]. 循证医学, 2013, 13(03): 181-184, 188. [本文引用:1]
[13]	Discacciati A, Orsini N. Re: Coffee consumption and risk of prostate cancer: An up-to-date meta-analysis[J]. Eur J Clin Nutr, 2014, 68(3): 409-410. [本文引用:1]
[14]	Lee PN. Simple methods for checking for possible errors in reported odds ratios, relative risks and confidence intervals[J]. Stat Med, 1999, 18(15): 1973-1981. [本文引用:1]

2015

0.0

周权, 李卉, 罗美玲, 等. 剂量反应关系Meta分析在R软件中的实现[J]. 现代预防医学, 2015, 42(5): 789-794.

目的介绍如何利用R软件中实现剂量反应关系的Meta分析。方法拟通过实例数据的演示,在R软件中,先利用Metafor程序包进行探索性二分类Meta分析,在得出意义结果的基础上再利用dosresmeta程序包进行剂量反应的Meta分析,并绘制非线性(和)或线性剂量反应曲线结果 R软件分析结果显示:饮酒是结直肠癌的危险因素,剂量反应关系的非线性检验P值处于临界水平(0.046)。非线性剂量反应模型显示:相对于最低饮酒量 (0 g/天),每日饮酒20 g、40 g、60 g发生结直肠癌的相对危险度为:1(0.93~1.1)、1.3(1.13~1.4)、1.5(1.26~1.9);线性剂量反应模型显示:在最低饮酒量 (0 g/天)的基础上,每增加12 g,发生结直肠癌的危险增加8%,非线性或线性剂量反应曲线图形基本相似。结论 R软件可以实现剂量反应关系的Meta分析,功能强大,实用性强。

... 剂量反应关系Meta分析是一类新型的Meta分析方法,相比常见的二分类及连续性资料Meta分析,此类研究可估计暴露因素与疾病的剂量反应关系^[1] ...

... 之前笔者所在研究团队已介绍过利用三种软件实现此类Meta分析的方法^[1,7,8],但在实际分析过程中,经常会遇到这样的情况:多数原始研究均以最低剂量组为参照组,而少数原始研究却以其它组别为参照,这两类研究是不能直接合并的,要合并就必须将少数以其它组别作为参照的原始研究转换为以最低剂量组作为参照的情况 ...

2012

0.0